A Synthesis Model With Intuitive Control Capabilities for Rolling Sounds


Authors: Conan S., Derrien O., Aramaki M., Ystad S., Kronland-Martinet R.
Publication Date: August 2014
Journal: IEEE/ACM Transactions on Audio, Speech, and Language Processing (vol. 22, pp. 1260-1273, 2014)
Tags: Environmental Sounds, Solid Sounds, Sound Design
Abstract
This paper presents a physically inspired source-filter model for rolling sound synthesis. The model, which is suitable for real-time implementation, is based on both qualitative and quantitative observations obtained from a physics-based model described in the literature. In the first part of the paper the physics-based model is presented, followed by a perceptual experiment that aims at identifying the perceptually relevant information characterizing the rolling interaction. This experiment enables us to hypothesize that the particular pattern of the interaction force is responsible for the evocation of a rolling object. A complete analysis-synthesis scheme of this interaction force is then provided, along with a description of the calibration of the proposed source-filter sound synthesis process. A mapping strategy that enables intuitive control of the proposed synthesis process (i.e. size and velocity of the rolling object and roughness of the surface) is finally proposed and validated by a listening test.
Introduction
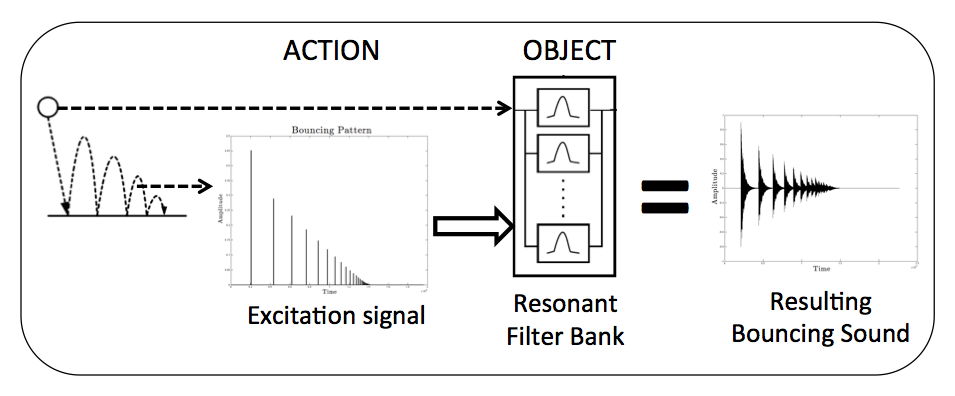
Previous studies proposed an intuitive control (i.e. coherent with human auditory perception) of impact sound synthesis, to create sounds by defining the sound producing object through verbal labels and morph between different impacted materials [1,2]. We want to extend these possibilities by proposing a control of the interaction with the sound producing object. The construction of the synthesis model is based on an action-object paradigm as proposed by Gaver [4]. This paradigm assumes that the object’s and the action’s properties can be modeled separately before they are combined. Perceptual auditory information related to the object’s properties such as shape and material are contained in the object’s eigenmodes (i.e. frequency, damping and amplitude of each partial) and can be modeled by a well tuned resonant filter bank (we use the filter implementation proposed by Mathews and Smith in [5]). This is the filter part of the model. The source part of the model simulates the action by a well defined time-varying signal which excites the filter. This concept is schematized in figure below.
Source signal models based on a similar approach have previously been proposed for rubbing and scratching sounds. The perceptual differences between these sounds have been evaluated by the present authors in [6], in order to define a mapping strategy to propose intuitive control and morphing possibilities between these interactions. In these models, the source is considered as a series of micro-impacts. The aim of the present study is to propose a source model evoking the rolling interaction. To do so, we consider a physics-based model from the litterature [7], and especially the interaction force between the rolling ball the surface on which it rolls; this force carrying the perceptual information about the rolling interaction. This is investigated through a perceptual experiment. Then, an analysis-synthesis scheme of this interaction force is proposed based on the assumption that the interaction force is a series of micro impact. Such a model should be sufficiently generic to enable continuous transitions towards other types of interactions such as rubbing or scratching. High-level controls of the synthesis model are finally proposed for the ball’s size and velocity and for the surface roughness, and validated thanks to a listening test.
Rolling Sound Synthesis Models: State of the Art
Details on the Physics-Based Model proposed by Rath et al.
The rolling sound synthesis model proposed by Rath et al. [7] is basicaly derived from a “bouncing model” which models the nonlinear interaction force f between a rigid sphere and a resonant object modeled as a lumped system, by a set of N second-order oscillators (mass-spring-damper systems) [8]:
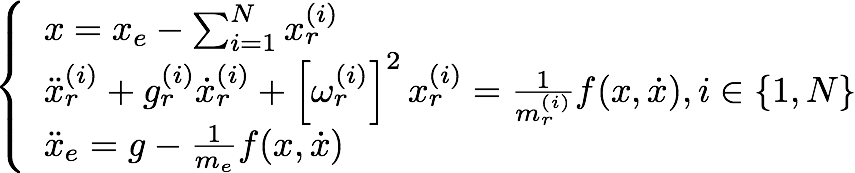
where Xe is the vertical displacement of the exciter (the ball), and Xr the vertical displacement of each second-order oscillator; and the resulting sound is the sum of the contribution of each second-order oscillator. X is the penetration of the ball into the resonant surface, and the other parameters are detailed in the paper. Such a model can generate bouncing sounds as below.
In order to adapt this nonlinear contact model to a rolling sound synthesis one, a dynamic offset signal is added to the distance variable x. This signal, which is used to “feed” the impact model, is derived from physical considerations. Indeed, by considering the surface Sr on which the ball rolls as imperfect (i.e. not perfectly smooth on a micro-scale, as it is for real surfaces), one can assume that the rolling ball has a vertical movement along its trajectory and hits a certain number of asperities, depending on its size (e.g. the bigger the ball, the fewer the asperities and hence, the fewer the impacts). This vertical displacement (Xoffset) is added to the distance variable X, and is called the offset-curve (see the figure below).

Examples of sounds generated with the model:
Perceptually Relevant Cue for the Rolling Evocation
A listening test was performed to evaluate whether, depending on the chosen parameters, the interaction force alone can evoke the rolling interaction.
Auditory stimuli are available here.
Proposed Model
The previous test revealed some combinations of parameters enabling the interaction force to evoke the rolling interaction. The raw force can be used as a source signal in our source-filter model.
Hence, we propose a signal model enabling the evocation of rolling interaction, based on an analysis-synthesis scheme of the interaction force.
Signal Characterization of the Interaction Force
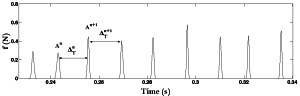
As one can note on the figure below, the interaction force can be considered as an impact series.
We propose to consider the interaction force with the formalism below.
with
and Φ is the impact pattern (i.e. the shape of each impact).
We propose an analysis-synthesis scheme that can generate forces as impact series by adjusting the statistics of the series of amplitude (A) and time intervals (ΔT) between impacts.
Analysis-Synthesis Scheme
The figure below illustrates the analysis-synthesis scheme. The impact model, and its dependence with impact amplitude, in the synthesis scheme is derived from physical studies [doel,8,9] and simulations. Note the amplitude modulation in the synthesis scheme, devoted to enhance the rolling object’s speed.

The impact model is a raised-cosine [11]:
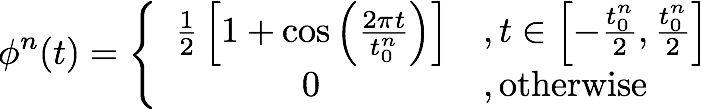
where the impact duration t0 depends on the impact amplitude:
Sound examples of the analysis-synthesis approach (no amplitude modulation is considered).
Additional Material: velocity and amplitude modulation
Download:
Additional figures regarding parameters evolution with velocity
Additional sounds with different velocity
In the soundfiles name, the label “V= ” is the velocity in centimeters per sec. One can note that the velocity difference between 2 sounds is poorly conveyed.
Additional Material: Parameters estimation
Download:
Additional figures for the residual modeling
Likewise the paper, when not varying, the parameters are κ=κ2, μ=μ2 and β=-0.5. Left column is the amplitude, right column ΔT.
Subjective Evaluation
The sounds used during the subjective evaluation of the synthesizer’s mapping are available here.
Video demonstration of the real-time synthesizer
Conclusions and Perspectives
Based on a paradigm action-object, that assumes that the exciter (the ball) and the resonant surface are decoupled, we proposed a source-filter model for rolling sound synthesis. The source, carrying the auditory information about the interaction (to roll), is modeled thanks to the analysis of a physics-based model previously proposed [7], and the filter part, carrying the information about the resonant object, is based on previous work by Aramaki et al. [1],[2] and is currently implemented using a resonant filter bank as proposed by Mathews and Smith [5]. Some high-level controls such as ball’s velocity, mass and surface roughness were proposed and validated thanks to a perceptual experiment. The source modeling for rolling sounds synthesis is generic enough to synthesize other kinds of continuous interaction sounds such as scratching and rubbing, and we already proposed a control interface that allows to morph continuously between rubbing, rolling and scratching [3] (video demonstration available at: http://www.lma.cnrs-mrs.fr/~kronland/InteractionSpace/).